ATTENTION - Cet article fait référence à Eos, le calculateur qui a précédé Olympe à CALMIP
Objectifs :
- établir le lien entre les performances de calcul et la bande passante mémoire
- mettre en évidence le lien entre l’efficacité de la vectorisation et l’intensité arithmétique(1).
Environnement de test
Chacun des tests a été effectué à travers la réservation d’un nœud d’Eos.
Les modules suivant (et uniquement ceux-ci) sont chargés :
Currently Loaded Modulefiles: 1) intel/16.1.3 2) vtune/2016.1.3
L’ensemble des sources utilisées dans cet article sont disponibles ici.
Vectorisation d’une boucle simple
On étudie la boucle de calcul suivante (i.e. Programme n°1) :
integer, parameter :: n=655360000
real(kind=8), dimension(n) :: a_vec, b_vec, c_vec, d_vec, e_vec
...
do i=1,n
a_vec(i)=b_vec(i)*c_vec(i)+d_vec(i)*e_vec(i)
enddo
Les données générée par ce programme occupent un espace mémoire d’environ 24 GB en RAM.
On effectue le calcul dans deux configurations différentes : scalaire (option de compilation -no-vec) et vectoriel (option de compilation -xAVX).
Le rapport de compilation confirme l’absence de vectorisation dans le premier cas.
LOOP BEGIN at vect.f90(34,14) remark #15540: loop was not vectorized: auto-vectorization is disabled with -no-vec flag remark #25438: unrolled without remainder by 4 LOOP END
Les instructions de vectorisation sont bien appliquées sur la boucle en question dès lors que l’option -xAVX est utilisée.
LOOP BEGIN at vect.f90(34,14) ... remark #15305: vectorization support: vector length 4 remark #15300: LOOP WAS VECTORIZED ... LOOP END
On recueille les temps de calcul suivants :
-no-vec |
-xAVX |
| 2,36 s | 2,38 s |
On voit donc que même si la vectorisation (AVX) devrait théoriquement apporter un gain sur le temps de calcul (vecteurs de quatre réels double précision), il n’en est rien en pratique.
Il se trouve que cette boucle nécessite le traitement de quelques milliards d’opérations (environ 3 GFlop). La vitesse de traitement de cette dernière est donc comprise entre 1 GFlop/s et 1,5 GFlop/s, ce qui est très en deà§à de la capacité théorique du cœur de calcul (22 GFlop/s).
Hypothèse : Le CPU est sous-exploité, c’est la bande passante mémoire qui limite les performances. La vectorisation n’est pas efficace dans ce cas.
Bande passante mémoire
Il se trouve que le nœud de calcul utilisé (Eos) a une architecture bi-socket, i.e. deux processeurs alimentés chacun par un bus mémoire depuis la RAM. Le calcul scalaire réalisé n’exploite qu’un seul socket, donc un seul canal mémoire.
On va alors à présent utiliser les deux sockets du nœud afin de doubler la bande passante mémoire par rapport au test précédent. On s’attend donc à une amélioration des performances.
Pour cela on se propose d’activer OpenMP sur cette boucle. En utilisant une stratégie "First Touch" sur les deux sockets d’un nœud (placement des threads au plus près de la mémoire allouée par ces derniers), on utilisera toute la bande passante mémoire disponible.
Le calcul est réalisé avec dix threads OpenMP.
On compare le cas compact (un seul socket utilisé), avec le cas scatter (deux sockets utilisés : doublement de la bande passante mémoire).
En secondes:
-no-vec |
-xAVX |
|
compact |
0,65 s | 0,54 s |
scatter |
0,33 s |
0,28 s |
En Gflop/s:
-no-vec |
-xAVX |
|
compact |
3,04 GFlop/s | 3,64 GFlop/s |
scatter |
5,88 GFlop/s | 6,93 GFlop/s |
On s’aperà§oit que le fait de doubler la bande passante permet d’augmenter d’autant la vitesse de traitement de la boucle. C’est bien la bande passante mémoire qui limite les performances : on dit que le code est "Memory Bound".
On reste néanmoins très en deà§à de la vitesse de traitement théorique du processeur (220 GFlop/s pour l’ensemble des dix cœurs).
Intensité arithmétique et vectorisation efficace
Étant donné que le Programme n°1 est limité par la bande passante mémoire (faible intensité arithmétique), nous allons étudier un second programme dont l’intensité arithmétique est plus importante.
Les calculs effectués sont à présent séquentiels (un seul cœur).
| Intensité Arithmétique = (# Flop) / (# Bytes) |
Cela revient à augmenter le nombre d’opérations effectuées pour chaque octet déplacé depuis ou vers la mémoire.
Prenons par exemple le cas suivant (ie. Programme n°2) :
do i=1,n
a_vec(i)=b_vec(i)*c_vec(i) &
+b_vec(i)*d_vec(i) &
+b_vec(i)*e_vec(i) &
+c_vec(i)*d_vec(i) &
+c_vec(i)*e_vec(i) &
+d_vec(i)*e_vec(i)
enddo
Par rapport à la boucle précédente, l’intensité arithmétique passe de 0,075 Flop/B à 0,275 Flop/B.
| (3 Flop) / (5 * (8 B)) = 0,075 Flop/B |
| (11 Flop) / (5 * (8 B)) = 0,275 Flop/B |
Les tableaux ci-dessous synthétisent les vitesses de traitements correspondantes.
en secondes:
-no-vec |
-xAVX |
|
Programme n°1 (0,075 Flop/B) |
2,36 s | 2,38 s |
Programme n°2 (0,275 Flop/B) |
2,34 s | 2,34 s |
en GFlop/s:
-no-vec |
-xAVX |
|
Programme n°1 (0,075 Flop/B) |
1,03 GFlop/s | 1,48 GFlop/s |
Programme n°2 (0,275 Flop/B) |
2,58 GFlop/s | 4,15 GFlop/s |
On voit que l’augmentation de l’intensité arithmétique a eu deux effets majeurs :
- une vitesse de traitement plus élevée,
- une meilleure efficacité de la vectorisation.
Le Roofline model
Pour aller plus loin, on étudie le comportement de différentes boucles itératives d’intensité arithmétique croissante (cf. code source).
La figure ci-dessous illustre alors la vitesse de traitement de chaque boucle (axe des ordonnées) en fonction de son intensité arithmétique (axe des abscisses).
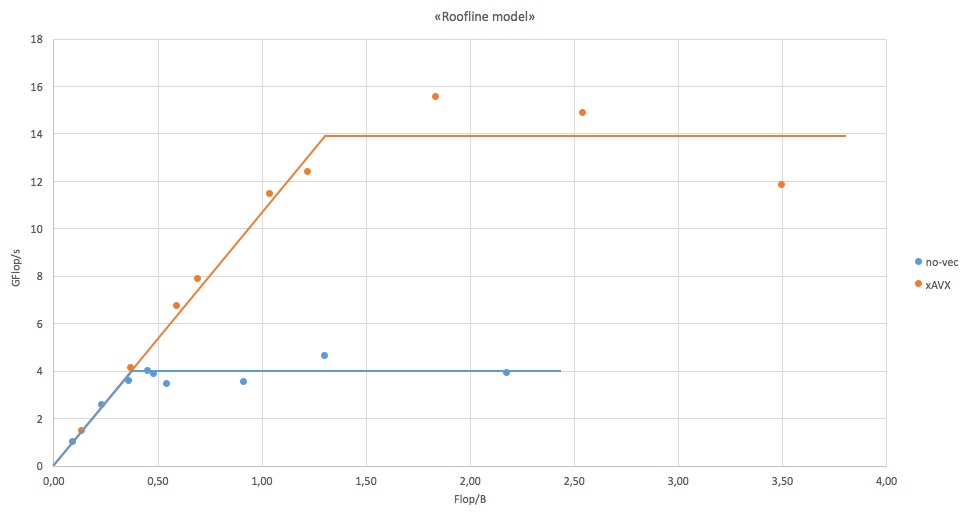
Plus l’intensité arithmétique augmente, plus la vectorisation est efficace : le CPU est de moins en moins contraint par la bande passante.
Ces courbes illustrent un phénomène propre à l’architecture en question, souvent cité au travers du terme "Roofline model":
- tant que le CPU n’est pas saturé, c’est la bande passante mémoire qui limite la vitesse de traitement. Que l’on soit dans le cas scalaire ou vectoriel, la relation entre l’intensité arithmétique et la vitesse de traitement est linéaire et ne dépend que de la bande passante utile (partie linéaire des courbes), on dit que le programme est "memory bound".
- Dès que l’intensité arithmétique atteint une valeur suffisante pour saturer le CPU, un pallier est atteint. Il correspond au pic utile du processeur, on dit que le programme est "CPU bound".
Voir ici pour la publication de Alexandar Ilic et al sur le "Cache-aware roofline model"
Conclusion
Afin de tirer partie de la puissance de calcul du processeur, ces exemples montrent qu’il est nécessaire de maximiser autant que possible l’utilisation d’une donnée au sein d’un noyau de calcul : voir l’exemple d’Intel pour un schéma de différences finies 3D.
(1) Intensité arithmétique : rapport entre le nombre d’opérations effectuées et la quantité de données mise en jeu (exprimée en Flop/B). Cette notion s’applique en générale à un noyau élémentaire de calcul.
